Welcome to Research Journal of Computer Science and Engineering

Abstract

The use of local fractional calculus has increased in different applications of image processing. This study proposes a new algorithm for image denoising to remove Gaussian noise in digital images. The proposed algorithm is based on local fractional integral of Chebyshev polynomials. The proposed structures of the local fractional windows are obtained by four masks created for x and y directions. On four directions, a convolution product of the input image pixels with the local fractional mask window has been performed. The visual perception and peak signal-to-noise ratio (PSNR) with the structural similarity index (SSIM) are used as image quality measurements. The experiments proved that the accomplished filtering results are better than the Gaussian filter.

Keywords: local fractional; Chebyshev polynomials; Image denoising

Introduction

The fractional calculus is extensively used in physical and engineering sciences applications for last 50 years. The fractional calculus has an important attention, especially in the field of image texture enhancement and image denoising [1-6]. Recently, local fractional has been applied in image processing for medical MR image enhancement [7]. As to our knowledge, no work has been done so far on image denoising based on local fractal. Image noise refers to any undesired signal that corrupts an image. Noise appears in digital images primarily by image acquisition, during which an optical image is converted into a continuous electrical signals.

Denoising is a significant pre-processing task for many applications like segmentation, texture analysis, and feature extraction. In previous work, fractional Conway polynomials with regularized fractional power parameters has been applied for image denoising [2]. The benefit of using fractional Conway polynomials is due to its ability to efficiently remove the image noise. In [3], an improved denoised algorithm based on fractional Alexander polynomials is proposed for removing different types of image noise. Experiments results showed that the fractional Alexander polynomials successfully removed the noise and enhanced the image details as well. Another image noise removal algorithm using both fractional Tsallis entropy with the fractional Riesz has been applied in [5,6]. The improvements achieved in removing image noise were compatible with standard image denoing filters like Gaussian, Kuan, and Homomorphic Wiener.

In this paper, we propose a new approach based on local fractional integral of Chebyshev polynomials [7] for image denoising. The rest of this study is organized as follows: in section 2, the proposed model is explained. In section 3, the experimantal results are described. Finally, the comparison with other methods and conclusion are presented in section 4, and section 5 respectively.

Proposed Model

Local fractional calculus (fractal) is an extension of differentiation and integration of the functions defined on fractal sets. The notion of local fractional calculus has been a subject of attentiveness, not only among mathematicians but also among engineers and scientists. There are various types of local fractional derivatives and local fractional integrals [8]. The proposed model is based on Gao-Yang-Kang definitions:

$I\left(\alpha \right)\left(x_0\right)=\underset{ x\to x_0}{\lim }\frac{{∆}^{\alpha }\left(I\right(x)-I(x_o\left)\right)}{(x-x_o)} \left(1\right)$           where

${\Delta }^{\alpha }(I\left(x\right)-I\left(x_0\left)\right)\right)=\Gamma (𝛼+1\left)\Delta \right(𝐼(𝑥)-𝐼(𝑥0))$

The local fractional integral is given by the following formula:

$J^{\alpha }𝐼(𝑥)=\frac{1}{\Gamma (𝛼+1)}\underset{∆\to o}{\lim }\sum _{i=o}^{N-1}𝐼\left({𝑥}_{𝑖}\right){∆}^{\alpha }\left({𝑥}_{𝑖}\right). \left(2\right)$

In this study, I and x represent the image and pixel value respectively. Note that the distance between two adjacent pixels is equal to one.

Proposition

For an interval [a,b], we have:${𝐽}^{\alpha }𝐼(𝑥)=\frac{{(𝑏-𝑎)}^{\alpha }𝐼(𝑥)}{𝛤(𝛼+1)}𝑥 𝜖[a,b]$)

In case of 2D image, we use ${𝐽}^{\alpha }𝐼(𝑥)\approx \frac{𝐼(𝑥)}{𝛤(𝛼+1)}$

The analytic form of the shifted Chebyshev polynomials is defined by the sum [9]

${𝑇}_{𝑁-1}(𝑥)=(𝑁-1)\sum _{i=0}^{N-1}{(-1)}^{N-1-i} \frac{(𝑁-2+𝑖)!}{(𝑁-1-𝑖)!(2𝑖)!}{𝑥}^i,$

Where b=1, and N>1. Applying (5) in (4), we get the local fractional integral of Chebyshev polynomials as follows [7]:

${𝐽}^{\alpha } {𝑇}_{𝑁-1}(𝑥)≔T_{N-1}^{\alpha }(𝑥)\approx \frac{{𝑇}_{𝑁-1}(𝑥)}{𝛤(𝛼+1)}$

With the coefficients, in case of N=3, i=0,1,2,

${𝑤}_0=\frac{1}{𝛤(𝛼+1),}$

${𝑤}_1=\frac{2}{𝛤(𝛼+1),}$

${𝑤}_2=\frac{1}{2𝛤(𝛼+1),}$

These coefficients are used to enhance the images. The local fractional integral of Chebyshev polynomials (LFICP) for image denoising is Idf, which is computed from input image I_nd: I_df(x,y)=M*I_nd(x,y) where M is the window’s mask, and * is the convolution product. The filter window’s mask is represented by the coefficients w₀,w₁, and w₃. In this study, four masks are created in four directions as shown in Figure 1.

The pixels values of LFICP window’s mask are calculated by moving the window’s mask over the input image.

The proposed LFICP window’s mask image denoising can be summarized as follows:

i. Initialize the LFICP window’s mask using 3 × 3 pixel size.

ii. Define the appropriate values of α with the range of 0 ? α ≤ 1

iii. Apply the proposed LFICP in four directions over the input image.

iv. Use Gaussian smoothing filter (GSF) for comparison.

v. Calculate the PSNR , and SSIM for both GSF filter, and the proposed LFICP.

For color images, the same algorithm used for grayscale images is applied separately for each color components.

Experimental Results

In this section, we demonstrate the denoising performance of LFICP operator. Performance tests were implemented using Matlab 2017b on Windows 10. The two sets of images employed two grayscale images, and two-color images.

The window’s mask of proposed LFICP is considered to be operated with a 3×3 pixels’ window. The quantitative presentations of proposed algorithm were calculated by both PSNR, and SSIM measures [8]. The PSNR values for the different values of α, are reported in Fig. 2, when applying the proposed LFICP algorithm on “Lena” image with Gaussian noise σ values of 15, 20, and 25.

A large value of α value corresponds to a dramatic decrease in PSNR, and vice versa. Therefore, the optimal value of α represents the trade-off between α and PSNR which is required for removing the image noise. In this study, the value of α has been chosen equal to 0.2 as shown in Figure. 2.

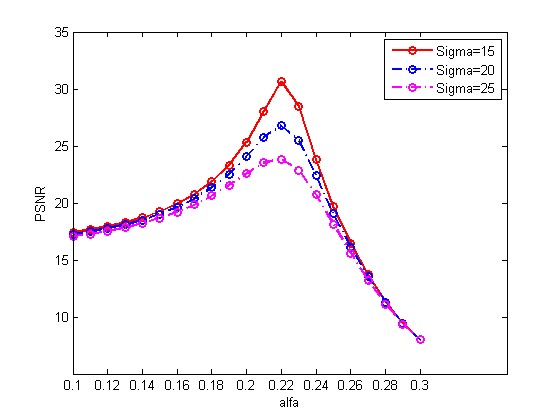
Figure 2: The values of α for Lena with σ values of 15, 20, and 25.

Figure 3: The denoised images of the proposed LFICP and GSF: (a) original image, (b) corrupted image with σ equal to 15, (c) Gaussian filter, and (d) the proposed LFICP filter.

Figure 4: The denoised images of the proposed LFICP and GSF: (a) original image, (b) corrupted image with Gaussian noise with σ value of 25, (c) Gaussian filter, and (d) LFICP filter.

The experimental image results of the four images are illustrated in Figure. 3 and in Figure. 3. Figure. 3(a) shows the original images, Figure. 3(b) shows the noisy images with σ = 15. Figure. 3(c) shows the denoised images after the Gaussian smoothing filter is used, while Figure. 4(c) shows the images after filtering using the proposed LFICP algorithm. Figure. 4 illustrates the same images for (a), (b), (c), and (d) but with σ = 25. Figures. 3, and 4 show that the proposed LFICP algorithm offers better performance for all tested images. The proposed LFICP algorithm removes the noise efficiently and saves the image texture details.

The PSNR and the SSIM values of the four tested images corrupted by two levels of Gaussian noise (σ = 15, 25) are shown in Table 1. In addition, Table 1 illustrates the numerical assessments of the proposed LFICP algorithm. The qualitative results illustrate that the proposed LFICP algorithm achieves the superior PSNR and SSIM values compared with Gaussian smoothing filter.

Comparison with other Approaches

To check the strength of the proposed LFICP algorithm, we compare the proposed study with other approaches for image denoising. Table 2 illustrates the results of the proposed LFICP algorithm with different denoising algorithms for the “Boat”, and “Lena” grayscale images with noise σ = 15 and 25.

In [11], a new image algorithm based on fractional integral is proposed for image denoising. This algorithm used the fractional calculus of Riemann-Liouville definition. In [12] the generalized Srivastava-Owa fractional integral operator was proposed for removing noise in images. Moreover, in [13], an approximate analytic solution for the fractional Cauchy-Euler equations was applied for image denoising by introducing a new fractional mask depending on proposed solutions.

Table 2 provides a general performance of different methods. These methods used different images with different noise σ. Table 2 shows that for image “Boat”, the PSNR values for the proposed LFICP algorithm are slightly larger compared with the three standard methods for the noise standard deviation σ of 15, 25. The proposed LFICP algorithm offered satisfactory results.

Conclusion

A new image denoising filter based on local fractional integral of Chebyshev polynomials for image denoising is proposed to remove Gaussian noise. The visual perception results with the PSNR and SSIM results are used to evaluate the denoising performance of proposed LFICP algorithm. Four standard test images were used to validate the performance of the proposed LFICP algorithm compared with Gaussian smoothing filter. The proposed LFICP algorithm has showed a good PSNR and SSIM results for all four testing images corrupted by Gaussian noise. In future works, we plan to apply the LFICP algorithm for different image processing applications like texture enhancement of digital images.

References

1. Obaiys, Suzan J, Eshkuvatov ZK, et al. 2013. On error estimation of automatic quadrature scheme for the evaluation of Hadamard integral of second order singularity. University of Bucharest. Scientific Bulletin. Series A. 1: 85-98. Ref.: https://bit.ly/2PVgbjE 

2. Hamid A, Jalab, Rabha W, et al. 2015. Fractional conway polynomials for image denoising with regularized fractional power parameters. Journal of Mathematical Imaging and Visio.51: 442-450. Ref.: https://bit.ly/2p02Snd 

3. Jalab HA, Ibrahim RW. 2015. Fractional alexander polynomials for image denoising. Signal Process. 107: 340-354. Ref.: https://bit.ly/2NKFy4Y 

4. Jalab HA, Ibrahim RW. 2013. Texture enhancement based on the savitzky-golay fractional differential operator.149289. Ref.: https://bit.ly/2NqCjAX 

5. Obaiys SJ. 2013. On the convergence problem of one-dimensional hypersingular integral equations. Mathematical Problems in Engineering. Ref.: https://bit.ly/2WVMSik 

6. Ibrahim RW, Hasan AM, Jalab HA. 2018. A new deformable model based on fractional Wright energy function for tumor segmentation of volumetric brain MRI scans, Computer Methods and Programs in Biomedicine. 163: 21-28. Ref.: https://bit.ly/2NP8tFa 

7. Obaiys SJZ, Eskuvatov NN, Long,et al. 2012. Galerkinmethod for the numerical solution of hypersingular integralequations based Chebyshev polynomials. 6: 2653-2664.

8. Xiao-Jun Y, Baleanu D, Srivastava HM. 2015. Local fractional integral transforms and their applications. Ref.: https://bit.ly/2NTxn6y 

9. Obaiys SJ, Putra Malaysia. 2016. On the General Solution of First-Kind Hypersingular Integral Equations. American Journal of Engineering and Applied Sciences. 2: 195-201. Ref.: https://bit.ly/2PUR68F 

10. Al-Shamasneh, A, Jalab HA, Palaiahnakote S, et al. 2018. A New Local Fractional Entropy-Based Model for Kidney MRI Image Enhancement. 20: 344. Ref.: https://bit.ly/33u6zk2 

11. Hu J, Pu Y, Zhou J. 2011. A novel image denoising algorithm based on riemann-liouville definition. 6: 1332-1338. Ref.: https://bit.ly/34HGWwm 

12. Ibrahim RW. 2011. On generalized Srivastava-Owa fractional operators in the unit disk. 1-10. Ref.: https://bit.ly/2Nqt0Rw 

13.Ibrahim. 2015. Image denoising based on approximate solution of fractional Cauchy-Euler equation by using complex-step method. 39: 243-251.Ref.: https://bit.ly/32tgLaU 

Download Provisional PDF Here